ポートフォリオ理論で出てくる、効率的フロンティアを描くコードを PyPortfolioOpt + Plotly で書いてみましたよという記事です。
まずは結果から。Plotly を使った動的なグラフなのでこちらのページをご覧ください。以下のようなグラフが表示されます。
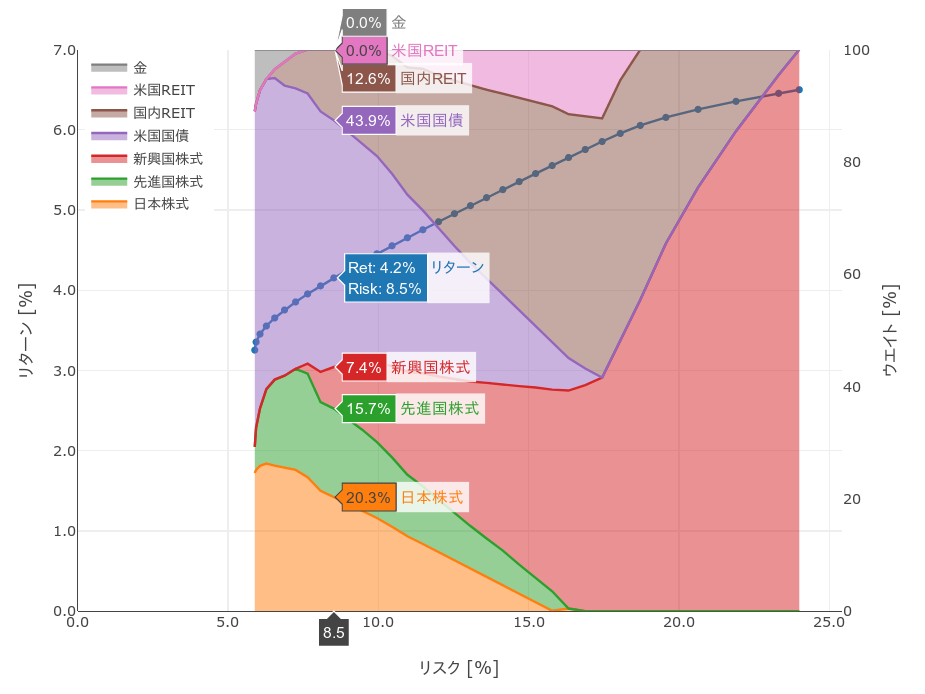青い点のある右上に伸びるカーブが効率的フロンティアのグラフです。その後ろにある積み上げグラフがそのリスクでの各資産の割合です。マウスオーバーすると細かい値が表示されます。
上記グラフで使ったリターン、リスク、相関係数は以下のページの値を拝借しました。
効率的フロンティアの書き方を調べていると、実はこの相関係数が非常に重要ということがわかりましたが、それは後述します。
資産運用を勉強していると必ず「卵は一つのカゴに盛るな」という分散投資の話が出てきます。1つのカゴを落としてしまっても、他のカゴの卵は守られる的な話です。ここまでは素人でも直感的に理解できますが、更に数学的にも裏付けられていて、リターン(期待値)とリスク(標準偏差)の異なる２つの銘柄(確率変数)があった時、それぞれが独立でない場合(相関がある場合)は、単品で保有するときよりも、分けて保有したほうがリスクを下がる可能性があります。
2つの確率変数 \(X,Y\) を足し合わせたときの期待値 \(E(X+Y)\) と分散 \(V(X+Y)\) は以下の公式になるそうです。
$$E(X+Y) = E(X) + E(Y)$$
この \(Cov(X,Y)\) は \(X,Y\) の共分散で、正の相関がある場合は正の値に、負の相関がある場合は負の値になります。このことから、負の相関を持つ銘柄を組み合わせると、個々の分散よりも小さくすることができます。
・・・余談ですが、高校の時に習った(そして忘れ去った)こういう公式も、こんな場面で役に立つんですね。当時もう少し勉強しておけばよかった。今となってはちょっと確率・統計系は勉強し直してもいいかもと思えてきます。
話は戻って、そして複数銘柄の全ての組み合わせの中で、あるリスクをとった時に最もリターンが高くなる組み合わせを効率的フロンティア(有効フロンティア)というそうです。
効率的フロンティアの図 (Wikipedia より引用 Copyright By Munasca)
まぁ、このあたりの説明はググれば大量に出てくるのでこのくらいにして、自分でも効率的フロンティアを求めることができるのかに興味がわきました。
調べてみると、Excelの「ソルバー」という機能を使って効率的フロンティアを求めることができるそうです。
ソルバーはこのページで初めて知ったのですが、Excelではこんなこともできるんですね。組み合わせが無限にある複数のパラメータを特定の制約条件下で振って、最適解を導く機能のようです。
普段 Linux を使っているので、わざわざこのために Windows を立ち上げ直すのが面倒なので LibreOffice Calc で試してみました。VBAが動かないのは予想していましたが、それ以前にソルバーの機能がExcelに比べて弱いらしく、そもそも答えを出せませんでした。
ソルバーの実装方法やソルバーライブラリなどを調べて、色々と迷い道をした結果、ポートフォリオ最適化用というそのものズバリのライブラリがあることがわかり試してみることにしました。
日本語の情報源としては以下のサイトが参考になりました。
最初に上のページを読んで概要を掴んだあとに、下のページと本家ページを見るとなんとなく使い方がわかってきます。PyPortfolioOpt は以下の図が示すように、以下の流れで効率的フロンティアを計算するようです。
- 何らかのデータ(上図左端の過去のデータや独自のモデル)を元に、期待リターン(Expected returns)と期待共分散行列(covariance matrix)を求める
- 期待収益率と期待共分散行列を元に効率的フロンティア最適化を行い結果を得る
今回は予め相関係数が分かっているものとして最適化させてみました。相関係数から共分散行列を求める方式です。コード中のパラメータは初心者が失敗しない株式投資入門さんのリターン、リスク、相関係数もの使用したものです。
スクリプトで生成した動的なグラフはこちら。長くなったのでグラフの考察は別エントリで書こうと思います。
#!/usr/bin/python3
import pandas as pd
import numpy as np
from pypfopt.efficient_frontier import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
import math
# 下記データは https://zog.jp/2332.html より
# 銘柄名
index = ['日本株式', '先進国株式', '新興国株式', '米国国債', '国内REIT', '米国REIT', '金']
# リターン
ret = np.array( [0.050, 0.055, 0.065, 0.025, 0.055, 0.050, 0.025])
# リスク
risk = np.array([0.175, 0.190, 0.240, 0.100, 0.190, 0.180, 0.160])
# 相関係数 (上三角のみ入力)
cor = np.array([[ 1.00, 0.70, 0.65, -0.50, 0.60, 0.50, 0.05],
[ 0, 1.00, 0.85, -0.40, 0.50, 0.75, 0.15],
[ 0, 0, 1.00, -0.20, 0.45, 0.65, 0.30],
[ 0, 0, 0, 1.00, -0.06, -0.01, 0.00],
[ 0, 0, 0, 0, 1.00, 0.40, 0.05],
[ 0, 0, 0, 0, 0, 1.00, 0.05],
[ 0, 0, 0, 0, 0, 0, 1.00]])
ret = pd.Series(ret, index=index)
print("== Return ==\n%s\n" % ret)
risk = pd.Series(risk, index=index)
print("== Risk ==\n%s\n" % risk)
cor = np.triu(cor, k=1) + np.triu(cor).T
print("== Correlation matrix ==\n%s\n" % cor)
cov = pd.DataFrame(
data = np.dot(np.diag(risk),np.dot(cor,np.diag(risk))))
print("== Covariance matrix ==\n%s\n" % cov)
ef = EfficientFrontier(ret, cov)
print("== Max Sharpe ==")
w = ef.max_sharpe()
perf = ef.portfolio_performance(True)
print("")
print("== Min Volatility==")
w = ef.min_volatility()
perf = ef.portfolio_performance(True)
print("")
import plotly
import plotly.plotly as py
import plotly.graph_objs as go
tret = np.arange(perf[0], np.amax(ret) + 0.001, 0.001)
res_ret = []
res_risk = []
res_text = []
res_weight = {}
for key in ret.keys():
res_weight[key] = []
for r in tret:
w = ef.efficient_return(r)
pref = ef.portfolio_performance()
w = ef.clean_weights()
print("Risk:%f, Ret:%f, Sharpe:%f %s" % (pref[1], pref[0], pref[2], w))
res_risk += [pref[1] * 100.0]
res_ret += [pref[0] * 100.0]
for k, v in w.items():
res_weight[k] += [v * 100.0]
data = [
go.Scatter(
x = res_risk,
y = res_ret,
hovertemplate = 'Ret: %{y:.1f}%
'
'Risk: %{x:.1f}%
',
name = "リターン",
mode = 'lines+markers',
showlegend = False,
yaxis = 'y1',
)]
for k, v in res_weight.items():
data += [dict(
x = res_risk,
y = v,
mode = 'lines',
name = k,
hovertemplate = '%{y:.1f}%',
stackgroup = 'weight',
yaxis = 'y2',
)]
axis_template = dict(
zeroline = True,
showgrid = True,
rangemode = 'tozero',
tickformat = ".1f",
hoverformat = ".1f",
)
layout = go.Layout(
xaxis = {
**axis_template,
'title': 'リスク [%]'
},
yaxis = {
**axis_template,
'side': 'left',
'title': 'リターン [%]',
'range': [0, math.ceil(max(res_ret))]
},
yaxis2 = dict(
title = 'ウエイト [%]',
side = 'right',
overlaying = 'y',
showgrid = False,
range = [0,100]
),
legend = dict(x = 0.01, y = 1.0),
)
fig = go.Figure(data=data, layout=layout)
plotly.offline.plot(fig,
filename='efficient_frontier.html',
show_link=False,
config={
"displayModeBar": False,
}
)