久しぶりに開発途中のネタです。
POI の最寄検索や、検索結果表示で現在値からの距離を表示させたくて、任意2点の緯度経度から距離を計算する方法を調べてみました。
地球が球体なら何となく頭をひねれば分かるかもしれませんが、楕円体の緯度経度から距離を求めるのは私には見当もつきません。
ということでググってみると、楕円体を考慮していて、世界中の緯度経度で通用しそうな計算式が2つ見つかりました。
何となく航海で使用する下の公式のほうが正確な気はしますが、上のヒュベニの公式の方が演算が簡単そうな気がします。
また、qgmapでは多少の誤差も許容できるので数%程度(?)の精度で十分です。そこで近似式も候補に入れてみます。
これらの計算式がどの程度の正確さなのか、ランダムに選んだ緯度経度で計算して誤差と計算速度を検証してみました。
とはいえ、検証しようにも正解がわからないので、とりあえず国土地理院のサイトで2点間の距離を計算できるようですので、そのサイトとの誤差を調べました。つまり、実際に正確かどうかの検証ではなくて、国土地理院のサイトの公式に近いかどうかの検証です (^^;
で、結果は以下のとおり。
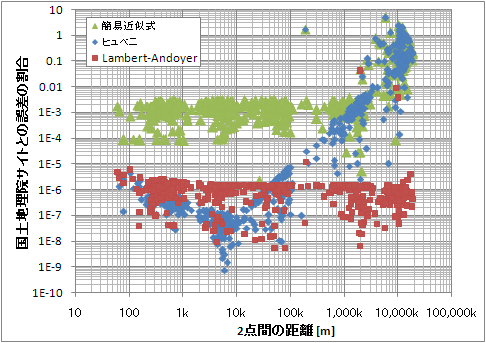
 アルゴリズムの違いによる国土地理院サイトとの誤差
アルゴリズムの違いによる国土地理院サイトとの誤差縦軸は国土地理院サイトで計算した距離(a)と、公式で計算した値(b)の誤差の割合(|a-b|/a) で、横軸が2点間の距離を示しています。
さすが航海算法と呼ばれるだけありLambert-Andoyerの公式は距離によらず 10^-5 以下の誤差率になっています。
ヒュベニの公式は50km以下ではLambert-Andoyerの公式と同等ですが、距離が離れるほど誤差が大きくなっていくようです。
簡易近似式は1000km以下では誤差0.1%前後で、1000kmを越えるとヒュベニの公式と同様誤差が増えていきます。
また、それぞれの公式を Zaurus で計算させた時の時間も測定しました。ちなみに、スペシャルカーネルを使っているので、浮動小数演算が高速化される FastFPE パッチが適用されています。
測地線航海算法のHPにはLambert-Andoyer と式的には同じですが、計算量が少し少ない小野の公式というものも載っていたので、こちらも計測しました。
各公式の計算時間
公式
|
1万回の計算時間 |
| 近似式 |
0.2838 sec |
| ヒュベニの公式 |
0.5043 sec |
| Lambert-Andoyerの公式 |
2.8202 sec |
| 小野の公式 |
2.6518 sec |
やはり近似式は演算量が少ないので高速ですね。1万回の計算が0.3秒なら充分実用的です。
ヒュベニの公式は近似式に比べ 1.8倍、Lambert-Andoyerの公式が10倍、小野の公式が9.5倍の時間がかかりました。
やはり精度が高い下の2つの公式は三角関数の演算などが多いため遅いですね。ただ、同じ結果が得られる小野の公式は少し早いようです。
結論
近似式が思いのほか精度が高かったので近似式を使おうと思います。
もともと精度も1%程度あれば十分かなと思っていたので、qgmap には充分ですね。
開発は案外こういう自己満足的な調査が楽しかったりするんですよねー。